Section 10 - Markov Models

Section 10 - Markov Models

States -
Transition Probabilities - chances of moving one state to another

Ex: Students who are Alert or Bored
There are some probabilities that student would transfer to the others

Simple Markov Model

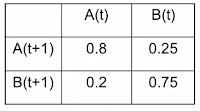
Use student example above with
20% of alert students become bored
25% of bored students become alert

Assume 100 alert and 0 bored  ==> 20 become bored, 80 stay alert
equilibrium is difficult to calculate

Use a Markov Transition Matrices as follows:

After a number of period it reaches at equilibrium @ ~58%

 

Now we want to calculate what the values at equilbrium more directly.  Here is what the calculation looks like.  (NOTE - the step in the middle he is just multiplying everything by 20)

 

 

  so P = 5/9 = 55.6%

 

Markov Model of Democritization

Initial Example
Assume democracies and dictatorships, where 5% of democracies becomes dictatorships, and 20% of dictatorships become democracies.

 

Model Involves Countries
Free, Not Free, Partly Free
Rules: 5% of free and 15% of not free become partly free, 5% of not free and 10% of partly become free, 10% of partly free become not free.  Leaving the follow matrix

 

Markov Convergence Theorem

Tells us that, if the transition probabilities stay fixed, the systems will lead us to an equilibrium

Four assumptions of Markov Processes

1.  Finite Number of States
2.  Fixed transition probabilities
3.  You can eventually get from any state to any other
4.  Not a simple cycle

Given 1 - 4 the process will converge

• this says the initial state doesn't matter
• History doesn't matter either
• Intervening to change the state doesn't matter in the long run

Interventions may be helpful as it may take a long time to get back to equilibrium

Why would transitions probabilities need to stay fixed?  Our interventions need to affect the transition properties in the right direction.

Exapting the Markov Model