Section 10 - Markov Models

Section 10 - Markov Models

States -
Transition Probabilities - chances of moving one state to another

Ex: Students who are Alert or Bored
There are some probabilities that student would transfer to the others

Simple Markov Model

Use student example above with
20% of alert students become bored
25% of bored students become alert

Assume 100 alert and 0 bored  ==> 20 become bored, 80 stay alert
equilibrium is difficult to calculate

Use a Markov Transition Matrices as follows:

After a number of period it reaches at equilibrium @ ~58%

 

Now we want to calculate what the values at equilbrium more directly.  Here is what the calculation looks like.  (NOTE - the step in the middle he is just multiplying everything by 20)

 

 

  so P = 5/9 = 55.6%

 

Markov Model of Democritization

Initial Example
Assume democracies and dictatorships, where 5% of democracies becomes dictatorships, and 20% of dictatorships become democracies.

 

Model Involves Countries
Free, Not Free, Partly Free
Rules: 5% of free and 15% of not free become partly free, 5% of not free and 10% of partly become free, 10% of partly free become not free.  Leaving the follow matrix

 

Markov Convergence Theorem

Tells us that, if the transition probabilities stay fixed, the systems will lead us to an equilibrium

Four assumptions of Markov Processes

1.  Finite Number of States
2.  Fixed transition probabilities
3.  You can eventually get from any state to any other
4.  Not a simple cycle

Given 1 - 4 the process will converge

• this says the initial state doesn't matter
• History doesn't matter either
• Intervening to change the state doesn't matter in the long run

Interventions may be helpful as it may take a long time to get back to equilibrium

Why would transitions probabilities need to stay fixed?  Our interventions need to affect the transition properties in the right direction.

Exapting the Markov Model

Section 9 - Diversity and Innovation

Problem Solving and Innovation

Use Landscape to begin to get to the best value (hills and valleys)

Perspectives and Innovation

Perspective - how you represent a problem, to be able to encode it

Perspective - representation of all possible solutions, with encoding, by applying values, we get the landscape

Rugged Landscape - many peaks and valleys
Local Optima - peaks within the landscape
Mt Fuji - A landscape with one peak

Good Perspective - few local optima,

Shovel Size Landscape - by Taylor

Sum-to-Fifteen - Herb Simon
-  Cards 1-9 face up on the table
-  Player alternate selecting cards
- Win if you get to exactly 15

Magic Square - all rows add up to 15, all columns add up to 15 and all diagonals add up to 15

Savant Existence Theorem - for any problem there exists a Mt Fuji Landscape

Heuristics

Heuristics - how you move on the landscape (hill climbing, random search, etc)

Hill climb to get to local optima

Heuristic 1 - Do the Opposite - think about the current solution and do just the opposite
Heuristic 2 - Big Rocks First - Do important things first
Heuristic 3 - No Free Lunch (Wolpert  & McCready) - Algorithms that search the same number of points  with the goal of locating the maximum value of a function defined on a finite set perform exactly  the same when averages over  all possible functions
                  -  If you don't know if your perspective, no algorithm or heuristic performs better than any other.

Diverse heuristics provide better solutions

Teams and Problem Solving

Groups of people are better at solving problems - based on diversity of thought

Using Caloric Perspective
A = 10
B = 8
C = 6

Average = 8

Using the Masticity Perspective
A=10
B= 8
D =6
E = 4
F = 2

Average = 6

If they work as a team, then if they the person on Caloric finds C, then the person doing Masticity will not get stuck.  In this case the only place the team can get caught is A & B.

Claim: The team can only get stuck on solution that's a local optimum for every  member of the team.

So we want people with different perspectives and different heuristics

Assumptions
1) when you have a team, they are assumed to be able to communicate
2) There is some ability to recognize an error in our solution.  I propose something and people may actually not see the value.

Recombination

Recombination - take solutions from multiple problems, bring them together to recombine them to better and better solutions 

Innovation comes from recombination of many solutions.

How many ways to pick 3 objects from 10?

10 things to pick 1st, 9 to pick second, 8 to pick 3rd, .....

divided by 3 chances for 1st pick, 2 chances for 2nd, and 1 for third.

leaving 120 ways

Picking 20 cards from a deck ==> 52 x 51 x 50 x 49... / 20 x 19 x 18 x ...... leaving 125 trillion possibilities

Martin Weitzman - Recombinant Growth - whereby things continuously get recombined new growth. 

Ex: car - steering wheel, wheels, brakes, etc coming together to make a car.

Exaptation - some innovation comes up for one reason, but then gets applied to another.

Joel Mokyr - Gifts of Athena - how ideas are transferred from one location to another and between people.

Section 8 - Economic Growth

Exponential Growth

GDP -

X - dollars
r - % interest

X*(1+r) where interest is eventuall X*(1+r)^t (years)

Rule of 72 - Divide the growth rate into 72.  The answer gives you how many years to Double.

Continuous Compounding
If you show growth in infinitesimally small  time frames, the growth rate is:
        =  e^(rt)

Simple Growth Model

Economy
-  Workers
-  Coconuts
-  Machines
-  Machines wear out

Solow Growth Model

Bob Solow - Economist w/ MIT

Add A(t) which is innnovation

O(t) = A(t)K(t)^b*L(t)^*(1-b)

This will allow productivity to double

Will China continue to Grow?

The required Innovation to maintain 8-9% growth rates have never been seen.

So Chinas growth will be driven to show innovation and will likely only see 1-5%.

Why do some countries not Grow?

Botswana did well, while Zimbabwe didn't do so grow

- Strong government control is required to protect equpiment, etc.
- Too strong a central government (1-2 people), they will extract resources, which will reduce investment and lower incentive to improve.

Growth requires some Creative Destruction - old equipment isn't required as it is replaced by new.

Fertility
- Can't apply to trees or people.
- We can apply it to our own GDP.  If we don't innovate, we will slow our own growth.

Section 7 - Tipping Point

Tipping Points

Tipping points are different from Exponential Growth

Percolation Models

Does water percolate through soil
P - Probability of percolating
If P<59.2 then no percolation

Forest Fires

Percolating Banks
- Models failing banks - Generally you add more details for the banks, like assets, liabilities, etc.

Information Percolating
- If I pass a piece of information will it pass through to everyone

Works well for networks

Can work for technology

Contagion Models

SIS - Susceptible - Infected - Susceptible
Diffusion Model - uses a Transmission Rate - tau

what if 2 people meet
W = number of people  with Disease
(N-W) = number of people w/out Disease

tau(W/N)((N-W)/N) = probability of two people meeting and it spreading

Add the contact rate: c

multiple above by N*C

When W is small you get
When W = N/2

This is not Tipping, this is natural diffusion

SIS Model

Now once they get over the disease, they can get infected again

Just add a new factor to the end of the equation

     For SIS, we have added the -aW component which are cured people who can get infected again.
which can be simplified to:

     so for small Wt, then if ct>a, then disease moves on.  If ct<a the disease will not spread.

now call R(0) = ct/a,  if >1, then it spreads, if <1, then not  (R(0) is the basic reproduction number)

Classifying Tipping Points

Dynamical System

  In this graphi, there are 2 stable points, but the one labeled U is unstable and any small movement will push it one way or the other.

 

He will call this a "DIRECT TIP" - Small action or event has a large effect on the long run.

 

Contextual Tipping Points
- Where the environment changes forcing to a new class



Between/Within Class
Changing between classes

Measuring Tips

Utilize change in the likelihood of outcomes

Diversity Index - Social Science
-  Amount of Information
is based upon how different the outcomes are between the classes.

Diversity = Summation(1/Summation(P^2))


Entropy - from physics
-  Number of types
Entropy = - summation(P*log(2) (P))

Section 5 - Thinking Electrons: Modeling People

Section 5 - Modeling People

Thinking Electrons: Modeling People - Part 1

Purposeful Actors

Diversity

Rational Actor Models - Part 2

-  Assumes that people optimize their goals
-  Assumes an objective function (happiness, market share, votes, etc),  then they optimize

Start w/ an Objective  ==> Optmize  (i.e. maximize profit for a copmany, maximize utility for a person, political candidate get as many votes as possible)

revenue = Price x quantity
Qauntity = q, price = 50-q

What q maximizes the revenue

Decision - Objective only on what I do
Game - my payoff  is dependent on others in the game.  My payoff is decided by the action of others.

Normal Form Game

Model for 2 people going to the city or staying at home

In the case above, if person 1 stays at home they get a payoff of 1, regardless of person 2.  If person 1 goes to the city, they automatically get a payoff of 2.

For person 2, if they think person 1 is going to be rational, they should assume that person 1 will go to the city

Extension Form Game

Extensive Game Tree

Green person will decide to go with the 0,0, as if blue is rational then they will optimize and go after 3, if offered a choice.

When will we see rationality:

• When stakes are large.
• When things are repeated
• When groups make decisions
• When the problem is easy 

Rational assumes:

• Unique
• Easiest
• People Learn
• Mistakes Cancel out and you are left w/ rational

Behavioral Models - Part 3

-  Gather real data, then model people as close to how real people behave
-  Observe what people do, then find out that they are not rational, but they typically fit into some behaviors

2 books about how we add bias to our decisions
Daniel  Kahneman - Book - Thinking Fast and Slow
Richard Thaler - Book - Nudge

1. Prospect Theory - Decision based on having a known amount offered, but they will sometimes prospect.  We are risk adverse if the known amount is positive.  If the decision for negative amount first, then people will take the risk on b

2. Hyperbolic Discounting - Option A a $1000, wait until tomorrow $1005.  Short periods of time we won't tend to want a minimal increase.  We tend to allows ourselves to wait for a somewhat larger amount.

3. Status Quo Bias - we naturally want to keep the status quo,

4. Base Rate Bias - If you ask someone for a number, then ask them for a second number, they will tend to be closer

Problems w/ Biases
1.  Lots of Biases
2. WEIRD - Western Educated Industrialized Rich Developed Countries - Most biases are based on these categorized.
3. People Learn and can avoid
4. Biases can make things computationally difficult.

We want to consider which Biases have the most influence on the answer.

Rule-Based Models - Part 4

-  Assumes people follow rules
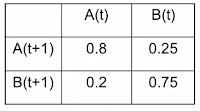
-  Schelling Model - example of a rule-based model

The matrix above is defines the various types of Rules-Based Models

We will walk through all 4 types

Fixed Decision Rule - may not be optimal
- Random decision choice
- Taken the most direct route - travel the most direct route -

Fixed Game
- Divide Evenly
- Tit for Tat - If you're nice, I'll be nice, etc. (Moore Machines)

     - Grim Trigger - if you are mean to me, I won't ever get over it.

Adaptive Decision Rule
-  Gradient method - I start by adding a certain amount, then slowly increasing until they start to get a little worse.
-  Random - I could randomly throw something in.

Adaptive Game/Strategies
-  Best Response - what is best possible response I can offer.
-  Mimicry - copy people who are doing well

Observation #1
-  Sometimes optimal rules are simple

Observation #2
-  Simple rules can often be exploited

So Why Model
-  they are easy to model
-  capture main effects
-  some of these models are ad-hoc, rules may not be representative
-  sometime rules can be exploited.

When Does Behavior Matter?

• Rational
• Behavioral
• Rules-Based

Deciding which one is best to use or if it even matters

Market - Two Sided (Buyers and Sellers)

Buyers have prices between $0 and $100

Sellers are willing to sell between $50 and $150

If you are the buyer you will start your price below, if you are a seller you will ask for a little higher than you would like.

Relevant buyers will want to buy between 50 & 100

Relevant sellers will have to sell between 50 & 100

rational will say about $75

optimizing won't change it much, so it will be about $75 again

Rules-Based again if you model you will likely find something around $75 again.

The market will not really change the model behavior

Game - Race to the bottom

Pick a number from 0 to 100, the person closest to 2/3rds of the mean will win

Rational would push us towards 0

Behavioral will ....

If you applied rules then you would be biased toward 50, then the best reponse is 2/3rds of 50 is 33, that should be my guess.

Irrational people will change things in this case.

Quiz 1

Quiz 1: Sections 2-4

Welcome to the first quiz! You'll be seeing one of these quizzes after every two new sections. They all have a mix of multiple-choice questions, numeric answers - in which you have to input a number - and "checkbox" questions, in which more than one option might be correct. You can take these a number of times, until you feel that you have the material down; just make sure you get it done before the close date! If you're having trouble understanding any concepts (or if you encounter technical problems), let us know about it in the discussion forum. And for those of you who feel like the quizzes are a breeze, check out the forum anyway, especially if you feel like helping out your peers!
The 12 questions on this quiz will cover sections 2, 3, and 4 (we're ignoring Section 1 for now). Here's what we learned:
Section 2: Segregation and Peer Effects
Section 3: Aggregation
Section 4: Decision Models
Questions on all quizzes will be both conceptual and technical; you'll be asked to think both broadly and precisely.
There are more questions on this quiz than on the rest you will take because we're covering 3 sections here instead of the usual 2. But don't worry, there's nothing here that we didn't talk about in the videos.
Good luck!

Question 1

Who developed the racial and income segregation model that we covered in section 2?

Answer for Question 1

Question 2

Recall that the index of dissimilarity is a way to categorize, numerically, how segregated a city is. Imagine a city comprised of four equal sized blocks. One block contains all rich people; one block contains all poor people; and two blocks contain equal numbers of poor and rich people. What is the index of dissimilarity? Answer using decimal notation.

Answer for Question 2

Question 3

Recall the standing ovation model. Suppose that in this case, perceptions of show quality are uniformly distributed between 0 and 100. Also suppose that individuals stand if they perceive the quality of the show to exceed 60 out of 100. Approximately what percentage of people will stand initially?

50

40

60

Question 4

In the Standing Ovation model, does increasing the variation in perceptions of quality always increase the number of people initially standing?

No

Yes

Question 5

Imagine a street on which there exist two sub shops: Big Mike's and Little John's. Each Saturday, Big Mike's draws an average of 500 people with a standard deviation of 20. Also on Saturdays, Little John's draws an average of only 400 people with a standard deviation of 50. If both distributions are normal, which shop is more likely to attract more than 600 people on a given Saturday?

Big Mike's

Little John's

Question 6

In the game of life, a world begins with 4 cells in a row in the alive state, and no other cells alive. After 20 updates, what state is the world in? (In other words, which cells are alive at this point?)

No cells are alive

The cells blink on and off

The same four cells are alive

There are six live cells in three rows

Question 7

Recall Wolfram's one dimensional cellular automata model. Which of the following classes of outcomes can this model produce? (Hint: pick more than one).

Randomness

Equilibrium

Complexity

Periodic Orbits/ Patterns

Question 8

Suppose that there exist three voters, each of whom is given three alternatives: A, B and C. There exist six possible strict preference orderings for these three alternatives: A>B>C, A>C>B, B>C>A, B>A>C, C>A>B, and C>B>A. The first voter has preferences A>B>C. The second voter has preferences B>C>A. Preferences of the third voter are unknown. How many of the six possible preference orderings, if selected by the third voter, would produce a voting cycle? (In a voting cycle, A defeats B, B defeats C, and C defeats A).

4

2

1

Question 9

Sarah is shopping for a computer. She researches different aspects of the computers for sale: screen size, processing speed, battery life, and special keys on the keyboard. For which of these attributes would Sarah likely have spatial  preferences?

Battery Life

Processing Speed

Screen Size

Special Keys on Keyboard

Question 10

You want to go to a concert in Detroit, but you have only $80. The cost of driving will be $30. When you get to the concert, there's a 40% chance you'll be able to get a ticket for $50, and a 60% chance that tickets will cost more than $50. If it's worth $130 to you to go to the concert, what's your expected value of driving to Detroit and trying to buy a ticket?

Answer for Question 10

Question 11

How many possible preference orderings exist for four alternatives? These orderings must satisfy transitivity.

Answer for Question 11

Question 12

Suppose that each of 400 people is equally likely to vote "yes" or "no" in an election. What's the size of the standard deviation for the total number of "yes" votes?

Decisioi Models - Sections 3 & 4

Aggregation (Lesson 3)

Philip Anderson - Physicist - Nobel Prize Winner - "More is Different"

-  Focuses on looking at systems vice components

-  One molecule of water isn't really wet, it takes many brought together.

Actions

Central Limit Theorem - Add Independent (Uninfluenced by others) Events - Probability Distribution

for Heads and Tails 

   if we have N events ==> mean = N/2

Binomial Distribution - more than 2 options (Not heads and tails)

pN where p is probability of something occurring

Mean = pN

SD  = sqrt(p(1-p)N)

sigma = Standard Deviation = -1 sigma to 1 sigma are seperated by 68%, where there are 2 standard deviations the probability increases to 95%, 3 sigma is 99.75%

Bimodal Distribution

2 peaks in the normal distribution

Six Sigma

Making production processes more predictable

- 3 Sigmas on either side of the mean - < 3.4 in a million

-  Single Rules

-  Family of Rules 

-  Preferences

Cellular Automata Models

Steven Wolfram is the original founder
Four Classes of Behavior in Automata Models

If you use the rules at the top, and start with the first row, then you get the follow-on rows.

  

Normative models - help us make better choices

Positive models - predict behavior of others

Classes of models
Multi-criterion models - selecting a car (many dimensions)

Qualitative Approach  - (create a table that help w/ the decision)(buying a house including sq ft, # bedrooms, # bathrooms, etc) and then filling it in.  Select where each one is better and count them up.

We can now add Quantitative Weights to each of the criteria

Spatial Choice Models
Probabilistic models - when you can compare x and y (fast and comfortable) and how far are we from an ideal point
Ideal Point - select a product closest to your ideal point.
You take the absolute value of the difference ==>  add them up and calc the distance

You can reverse this to explain what we are seeing.

Probability: The Basics
Axiom 1: any probability is between 0 and 1
Axiom 2: Sum of all outcomes is 1
Axiom 3: In an event, if one is a subset of the other, it's probability must be lower than the superset.

Types of probabilities
Classical probabilities (rolling dice, gambling, etc)
Frequency Probability (we look at data and estimate whether it will happen)
Subjective Probabilities (guessing, or using some subjective model)

Decision Trees
Decision Trees - yes/no trees leads to the value of information.  Good for model where there are lots of contingencies.

Scholarship: $5000
200 Applicants
2 Page Essay ($20 cost)
10 Finalists who will have to write a 10 page essay ($40 cost)
                                                 / Win (.1 chance) for 4940
                                  /Essay 2
              /  Selected                \ Lose (.9 chance) for -60
  /Essay                        \ Don't (-20)
X           \ Lose ( -20)
   \Don't start
   





Value of Information -